田中香津生

STEAM教育

物理

教育

大学

概要

近年、自ら問題設定し取り組むような教育としてPBL（課題解決型学習）が注目されています。「モデル化」というキーワードで文理問わず社会問題に取り組むようなPBL型授業として2018年に開講しました。様々な現象を理解して取り組むうえで、私たちは何らかのモデル化（数理モデル等）を行い、計算やシミュレーションなどを用いて検討していきます。ところが、中学～高校において既存のモデル化の手法（運動を、ニュートンの法則で記述する等）を機会が多くても、自ら妥当なモデルを設定する経験は中等教育～大学初等教育ではなかなかありません。そこで、この「モデル化」にフォーカスして受講学生のグループ主体的に一つの問題に取り組み、検証から提言まで行っていくプロセスをサポートしながら進めました。

この授業は4名が受講し、理系学部が2名、文系学部が2名でした。まずは学生に普段疑問に思っていることをブレスト式に一人あたり20個（合計80個）書き出してもらいました。以下はその一部です。

杜だい（川内の杜ダイニング）における、昼飯時の混雑の要因とは？なぜ解決されないか？
小説や本の一番最初の文章と本の評価との関連性
自分達が一日に発する言葉の量とその消費カロリー
私たちが直接的・間接的に一日に消費するCO2の排出量
国ごとに美的感覚が似ている理由
体育館の男子トイレは何故あんな形をしているのか
小麦粉の入ったボウルをひっくり返した後、粉は床にどのように分布するか
第二高校前の交差点はいつが一番混むのか？そしてスクランブル方式は本当に効率的なのか？
ゲームをする時、音楽（BGM）によって結果は異なるか？

この中で、生徒の中で相談した上で全員が関心を持って取り組めることができる「川内の杜ダイニングにおける、昼飯時の混雑の要因とは？なぜ解決されないか？」にフォーカスをして取り組みました。

食堂での調査

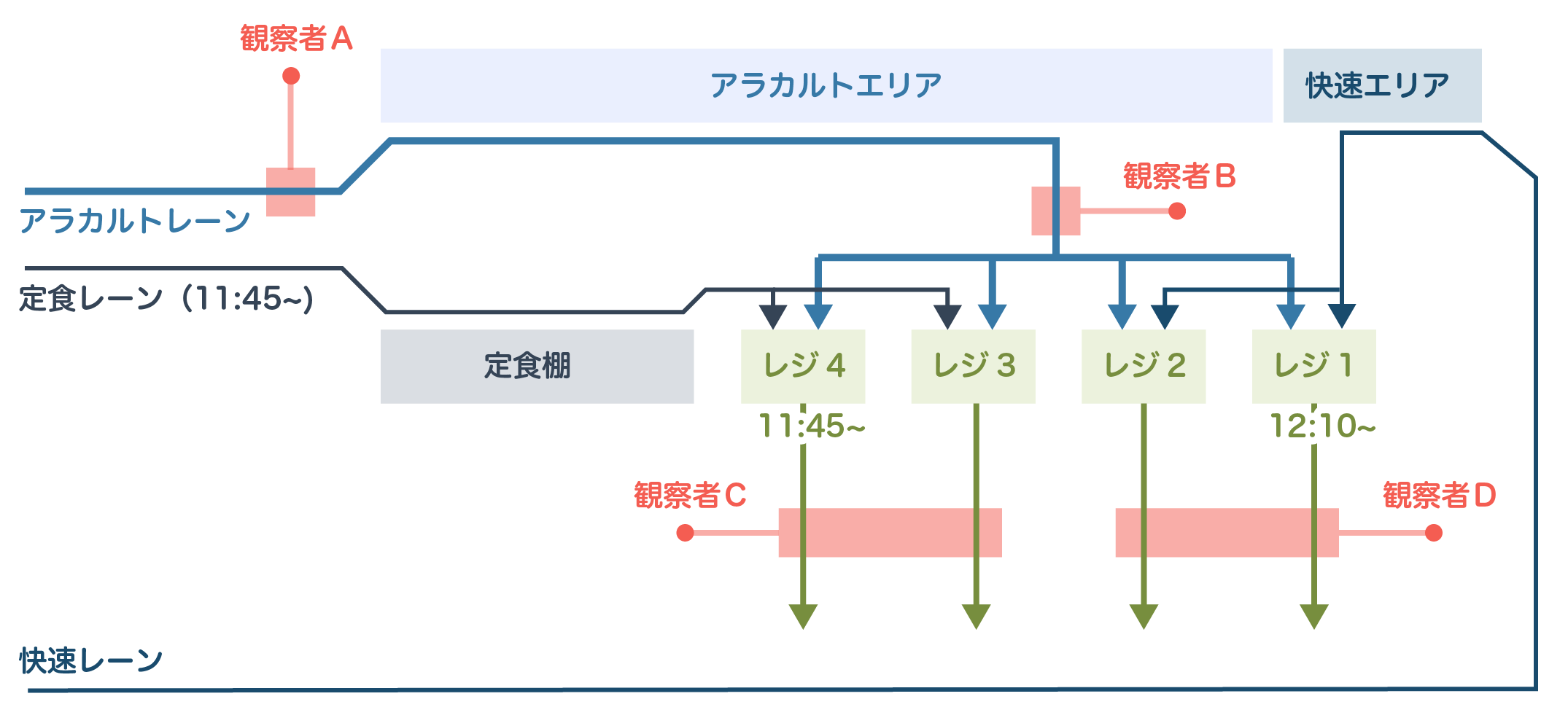
2018年5月23日のお昼の混雑時に４名の受講生とＴＡ１名で食堂の利用状況の観測を行いました。川内の杜ダイニングではアラカルトレーン、快速レーン（カレー等）、定食レーンと別れています。アラカルトレーンは昼食時に大変混雑するのに対して、定食レーンや快速レーンは比較的待ち時間が少なくすみます。レジは全部で４つあり、混雑に合わせてあけていました。特に混雑の要素となっているアラカルトレーンを重点的に下図のように各々が任意の場所における流入・流出人数を記録し、同時に後から詳しく調べられるように２台の定点ビデオ観測をする形をとりました。

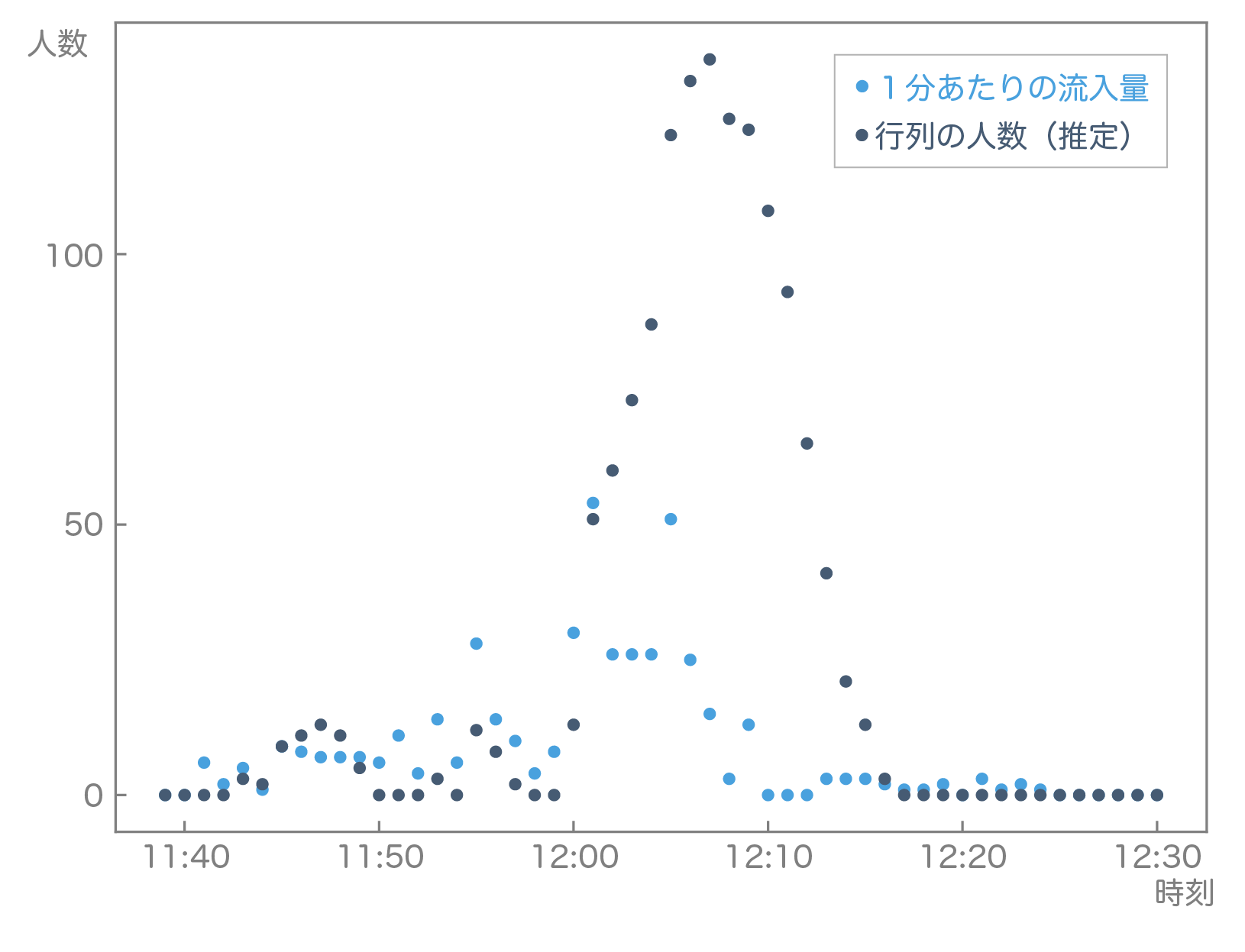
下図は調査結果のうちアラカルトレーンのものです。観測者Ａが計測したアラカルトレーンの流入量と、観測者Ｃ，Ｄによる流出量の差から求まる行列の人数の推定値をプロットしています。特に１２時～１２時１０分の間が流入量のピークで、１分あたり５０人を超える人数が列に並びます。また、行列の人数はこれに応答して１３０人を超えていました。

学生にこれらの計測から「何が最も行列の人数の支配的要因か？」について考え、議論してもらいました。候補として以下のようなものがあげられました。

レジでの処理速度がプリペイドカードを使用せず現金を用いている人によって大きく律速している。
渋滞緩和を目的とした定食レーンがほとんど使われていない。
４つ目のレジをあけたのが１２時１０分だったが、これが遅すぎるのではないか。
学食の特性上、流入量がお昼休憩直後の短い時間に大きなピークをもつためではないか

次に、これらの候補について簡易的な数理モデルを用いて定量的な議論・予測を行ってもらいました。一人の学生が一般的な待ち行列モデルを用いて十分議論ができるのではないかと提案し、以下のようなpythonコードを元に検討を行いました。

"""
 queue-simulation 待ち行列のシミュレーションコード
 展開ゼミ：課題解決型(PBL)演習A
"""

# モジュールのインポート
import numpy as np
import random
import matplotlib.pyplot as plt

#定数の宣言
MAX_CASHDESK = 4		#最大レジの数
NUM_CASHDESK_ARR = [2,2,2,2,2,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,4,4,4,4,4,4,4,4,4,4,4,4]
ENDSTEP = 2400		#シミュレーションが終了するまでに経過する時間（秒）

#計算用の配列の確保
queue_arr = np.zeros(MAX_CASHDESK, dtype=np.int)		#現在列に並んでいる人の数の配列queue_arrを初期化
time_arr = np.arange(ENDSTEP)		#グラフの横軸（経過時間）の初期化
queue_log = []		#列の並んでいる人数の経過ログの初期化
for i in range(0, MAX_CASHDESK+1):
    queue_log.append([])

t = 0		#経過時間（秒）の初期化


"""
関数
"""
def generation_prob(t):		#単位時間（秒）あたりに並ぶ人の数を返す関数
    #観測で得られた典型的なデータ
    GENERATION_RATE = 0.16		#１秒あたりに並ぶ人の数（適当な数字）
    #11:40-12:20における１秒当たりの並ぶ人の数（１分あたり、合計）
    flow_rate_all =[0.000 ,0.100 ,0.050 ,0.150 ,0.050 ,0.233 ,0.217 ,0.300 ,0.217 ,0.167 ,0.133 ,0.217 ,0.350 ,0.367 ,0.267 ,0.600 ,0.450 ,0.300 ,0.183 ,0.283 ,0.617 ,1.200 ,0.833 ,1.067 ,0.767 ,0.850 ,0.417 ,0.250 ,0.050 ,0.217 ,0.000 ,0.000 ,0.000 ,0.050 ,0.050 ,0.050 ,0.033 ,0.017 ,0.017 ,0.033 ,0.000 ]
    #11:40-12:20における１秒当たりの並ぶ人の数（１分あたり、アラカルトのみ）
    flow_rate_alacarte =[0.000 ,0.000 ,0.100 ,0.033 ,0.083 ,0.017 ,0.150 ,0.133 ,0.117 ,0.117 ,0.117 ,0.100 ,0.183 ,0.067 ,0.233 ,0.100 ,0.467 ,0.233 ,0.167 ,0.067 ,0.133 ,0.500 ,0.900 ,0.433 ,0.433 ,0.433 ,0.850 ,0.417 ,0.250 ,0.050 ,0.217 ,0.000 ,0.000 ,0.000 ,0.050 ,0.050 ,0.050 ,0.033 ,0.017 ,0.017 ,0.033 ,0.000 ]
    try:
        return flow_rate_alacarte[int(t/60)]		#１秒当たりの並ぶ人の数を返す
    except:
        return 0		#配列の範囲外だった場合は0を返す

def processing_prob(t):		#単位時間（秒）あたりにレジが処理する人の数を返す関数
    PROCESSING_RATE = 0.08      #１秒あたりにレジが処理する数（平均）
    cach_rate = 0.12     #現金で支払う確率
    #11:40-12:20における１秒当たりのレジが処理する人数（１分あたり、現金）
    process_rate_cash =[0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05]
    #11:40-12:20における１秒当たりのレジが処理する人数（１分あたり、現金）
    process_rate_card =[0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13,0.13]
    try:
        if random.random() < cach_rate: #
            return process_rate_cash[int(t/60)]        #現金での1秒当たりのレジが処理する人数を返す。
        else:
            return process_rate_card[int(t/60)]        #プリペイドカードでの1秒当たりのレジが処理する人数を返す。        
    except:
        return PROCESSING_RATE      #配列の範囲外の場合は平均値を返す


"""
シミュレーションのmain関数
"""
#シミュレーション開始tが0からENDSTEPまで繰り返す
while t < ENDSTEP:

    #並ぶ人がいるかチェック。いた場合は一番並んでない列に並べる
    if random.random() < generation_prob(t):
        queue_arr[queue_arr[:NUM_CASHDESK_ARR[int(t/60)]].argmin()] += 1
    #レジが処理できた人がいたかそれぞれの列でチェック。いた場合は列の人数を１つ減らす
    for i in range(0,MAX_CASHDESK):
        if random.random() < processing_prob(t) and queue_arr[i] > 0:
            queue_arr[i] -= 1
    #できた列をqueue_logにコピーする
    for i in range(0,MAX_CASHDESK):
        queue_log[i].append(queue_arr[i])
    #合計値をqueue_logの末尾に追加
    queue_log[MAX_CASHDESK].append(sum(queue_arr))
    #時間を進める
    t += 1

#結果をプロット
fig = plt.figure(figsize=(14,9))
#合計値をプロット
plt.plot(time_arr,queue_log[MAX_CASHDESK])
plt.xlabel('time(sec)')
plt.ylabel('queue')
plt.show()

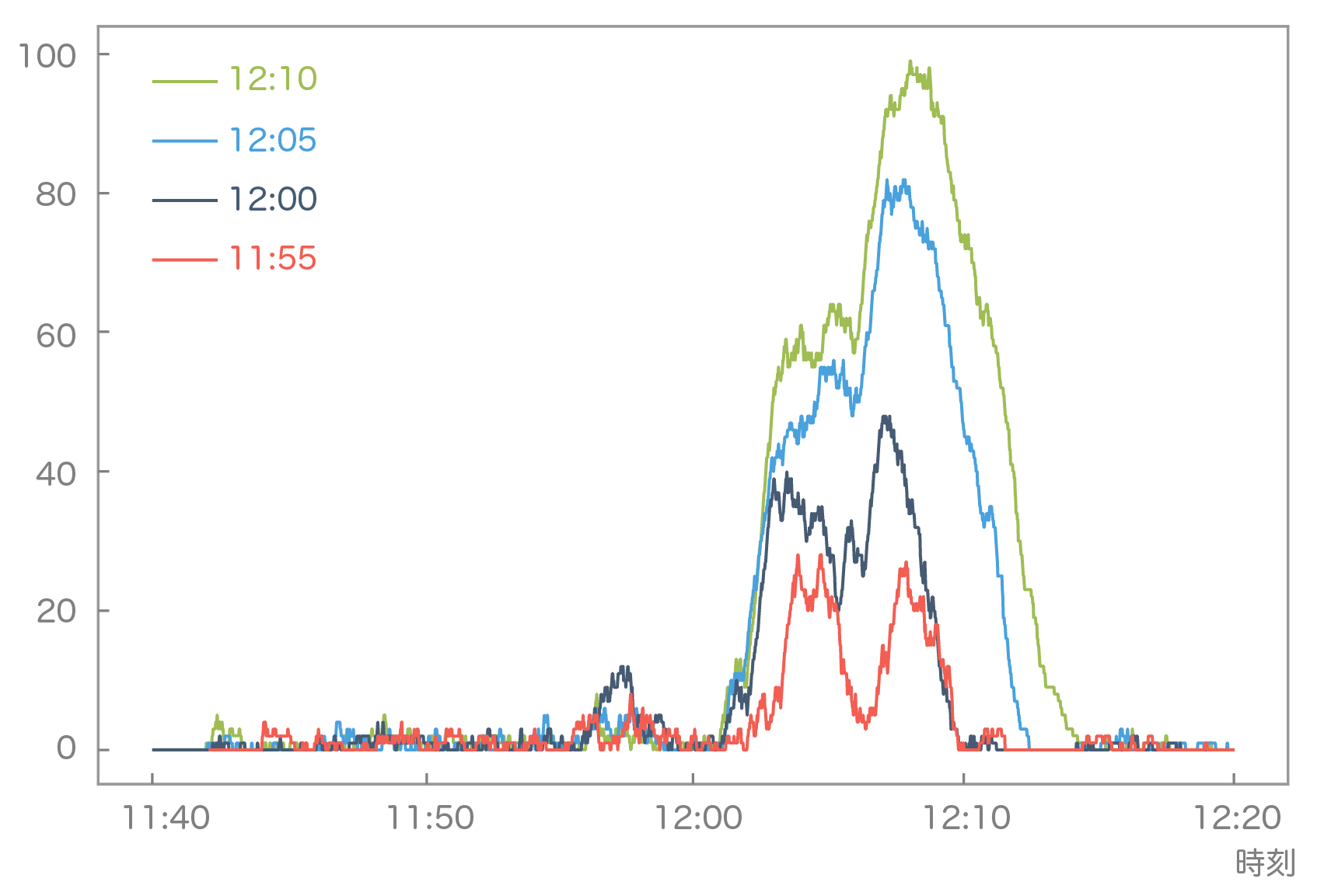
数はこのコードを元に「４つ目のレジをあけたのが１２時１０分だったが、これが遅すぎるのではないか。」を検討した例です。１２時１０分の結果は実際の観測した待ち行列人数の推定値の傾向と概ね矛盾がないことが分かり、また少しレジを開く時間を早くするだけで劇的に効果があることが分かります。

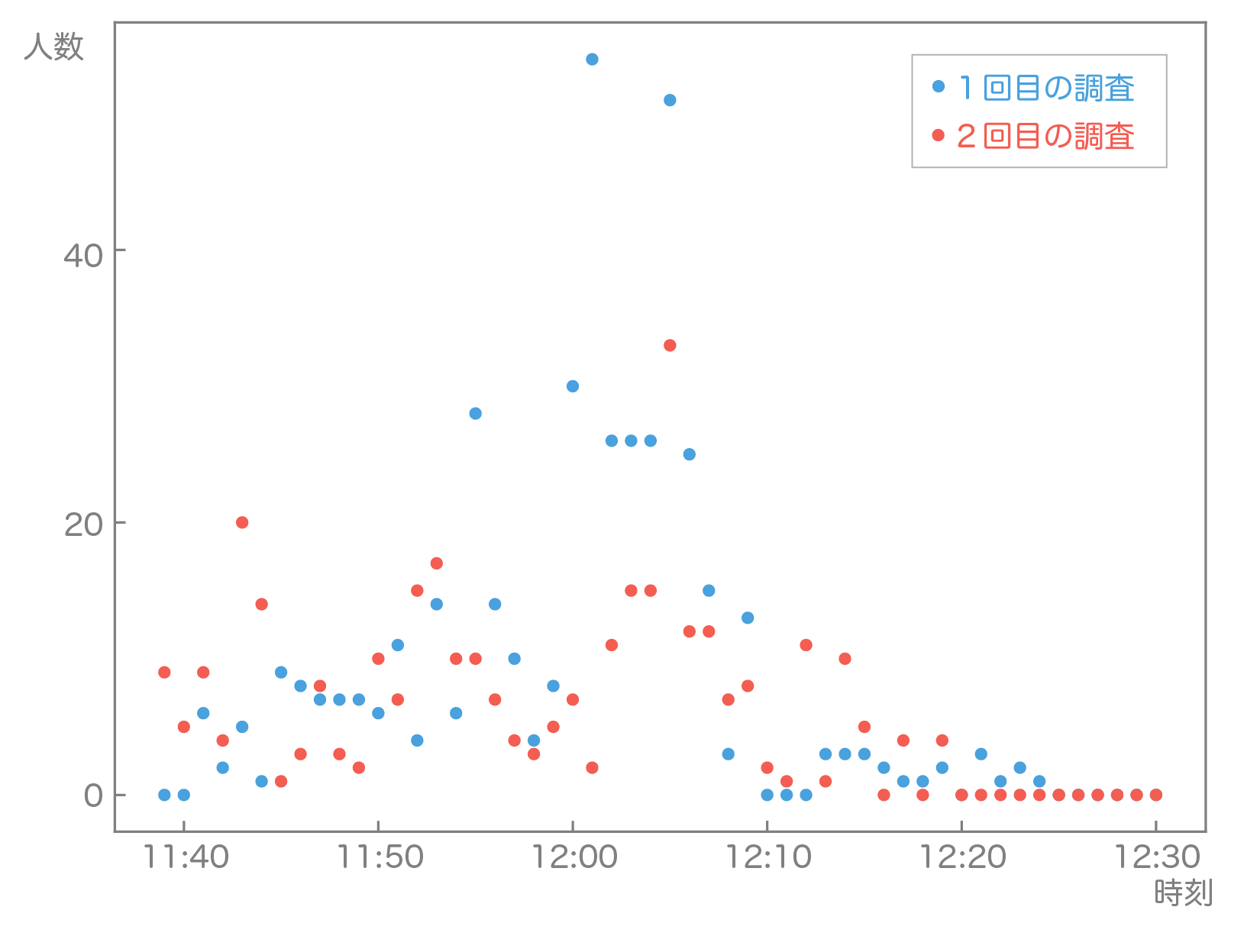
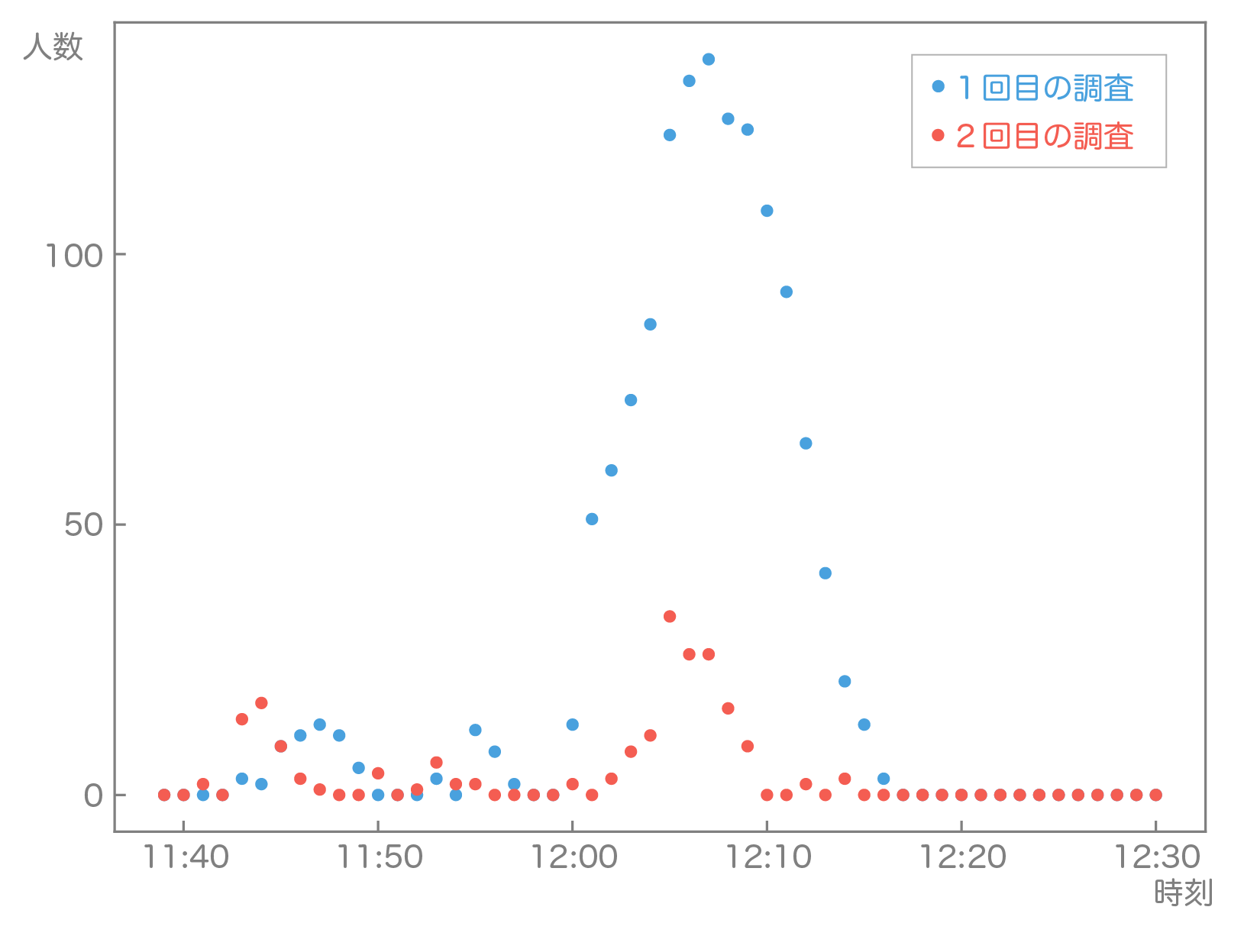
図７，８は１回目の観測と２回目の提案内容実施時の観測の比較です。図７はアラカルトレーンの流入量を表しています。２回目の流入量の合計はおよそ１回目のおよそ７割と、この日は相対的に来客数の少ない日でした。また、１回目に比べてピークが分散して１２時１０分以降にも継続的に流入があることがわかります。これはこの日たまたまの現象かもしれないですし、混雑時間啓発用ポスターの効果があったのかもしれません。いずれかは１回ずつの観測では残念ながら統計的に結論付けることはできそうにないです。一方図８の待ち行列の人数は顕著な違いがあります。１回目の観測では１３０名以上の人がピーク時に待っているのに対して、２回目はせいぜい３０名程度で、実際これまで建物の外まで長蛇の列が続いていたのに今回は目に見えて行列がなくなっていました。図７のように流入量が若干少なかったにせよ、それに対して十分有意な差があると考えられます。これはレジを有意に早く開けた効果が大きくあったと考えられます。また、この効果は図４のように待ち行列モデルを用いて定量的に検討した際のものとおおよそ同じ程度であることもわかりました。食堂のレジは一般的に人間が混み始めたと感じてから開けることが多いですが、それよりも一回り早く開ける工夫をすることで大きな効果が得られることが数理モデルによって実証できたことになります。

展開ゼミ 課題解決型(PBL)演習：科学の力で世の中をモデル化しよう

概要

食堂での調査

展開ゼミ　課題解決型(PBL)演習：科学の力で世の中をモデル化しよう