おうち実験
概要
高校の物理授業において、「自分で材料を集め、自宅で実験を行い、レポート書く」というおうち実験授業を実践しました。勤務校で行われている「実験室における実験授業」には以下の様な問題点を感じました。
- 授業時間内で完結させるため、必要な装置を事前に用意する。そのため、「この目的のためにはどの程度の道具がどの程度必要か」を見積もる経験が得られない。
- 授業時間内で完結させるため、実験手順をプリントで配りその手順にそって実験をさせる。そのため、「何をしたら目的となる検証になるか」といった、実験手法を考える経験が得られない。
- 授業時間内で完結させるため、実験結果を穴埋めプリントに記入させて提出させる。そのためレポート作成経験が得られない。
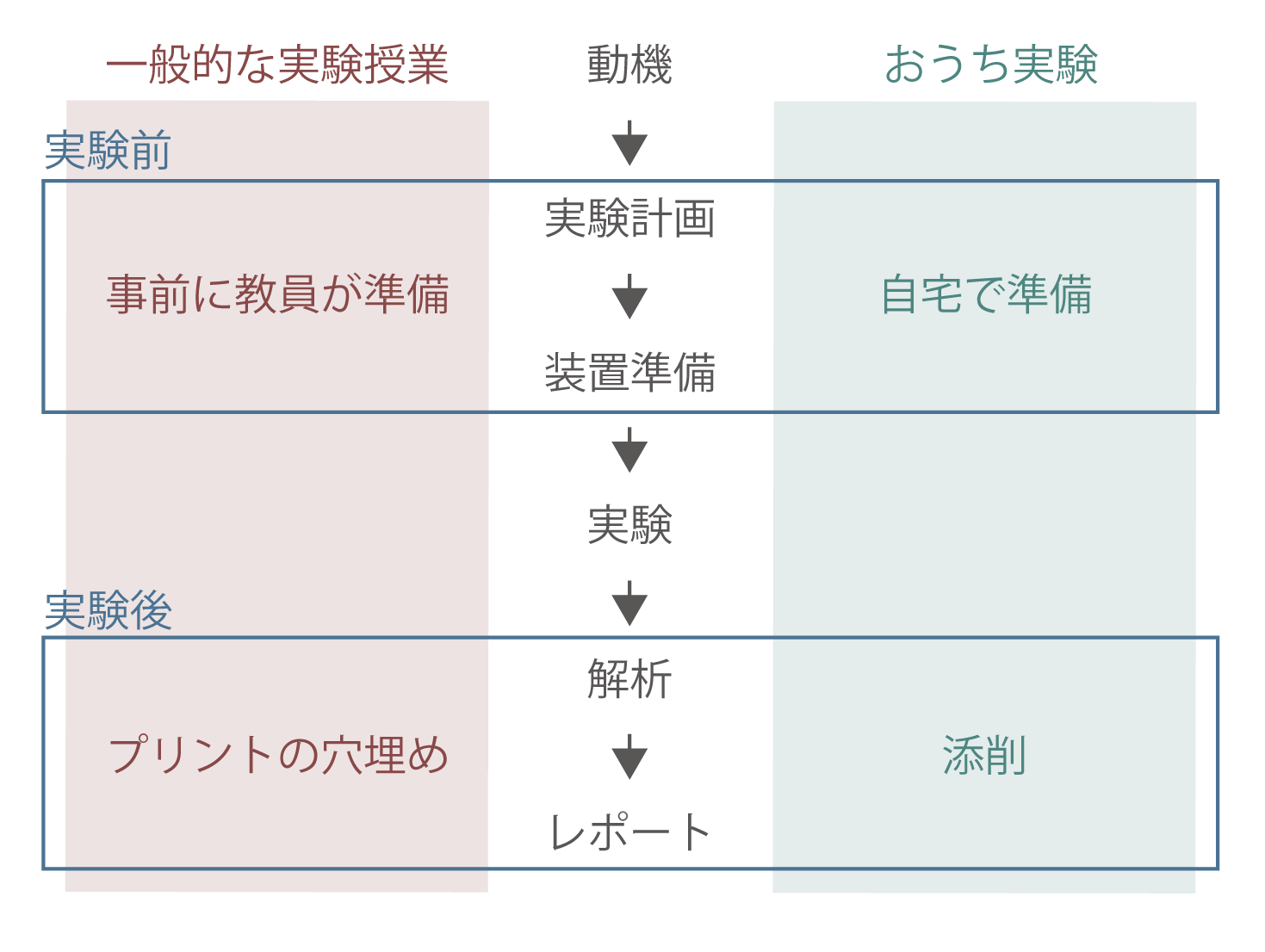
これらはいずれも授業時間と実験室が限られているために生じる問題です。そこで、各々がおうちで実験計画、道具準備、実験、レポート作成を完結させることができれば、本来目的としている「自らの疑問を解決する力」の養成になるのではと考えました。実施する上で以下の点について特に留意しました。
解析チェッカーの導入
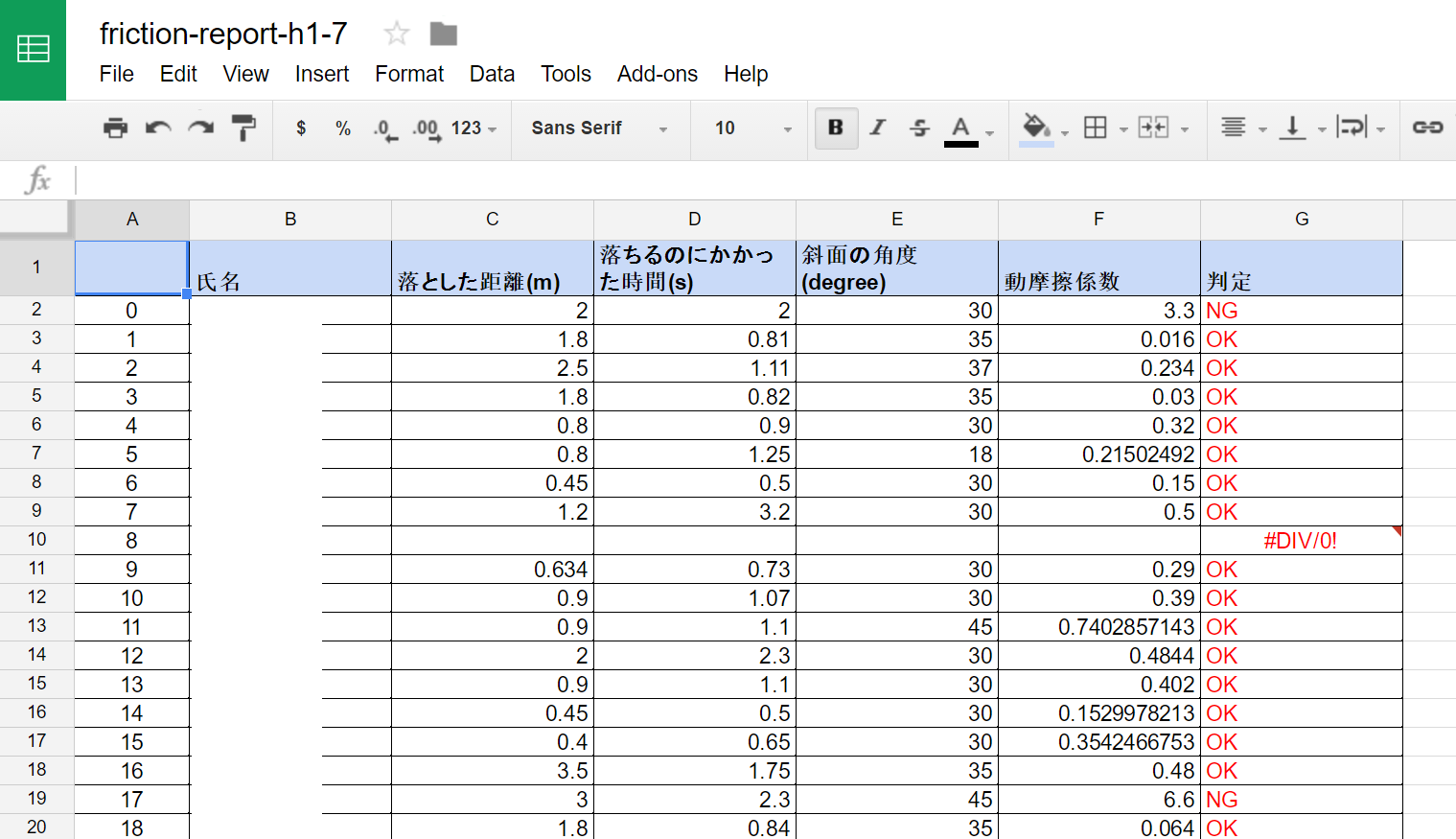
現象そのものではなく実験検証のトレーニングがメインなので、題材はできるだけ簡易でとっつきやすいものを選びました。自宅で全てを完結する場合、途中でどうすればいいかわからなくなってしまった時、フォローが難しいという問題があります。そこで、例えば解析が難しくなる場合は、ウェブ上で解析があっているかが自動で判別できるチェッカーを用意して、計算が苦手な生徒でもレポートの形にできるように工夫しました。解析チェッカーはgoogleのspreadsheetを用いて、他の生徒の状況も確認しながらチェックできるような仕組みにしました。
不確かさの評価
中等教育における実験授業では準備や手順が完了した状態で行うことが多いため、しばしば「どれだけ正確に実験ができたか」を目標にしてしまいます。例えば重力加速度の測定実験では数字を導出後に文献値と比較してその差が最も小さい実験が「いい実験」として評価されがちです。ですが、本来あるべき姿勢は目的の検証を行う上で必要な実験精度をおおまかに見積もり、その精度を達成できる実験手法を用意して実験を行い、最終的な測定値の不確かさを求めることで、実験値と文献値等と矛盾がないかを示すことです。そこで、実験準備の段階にある程度自由度を与え、工夫して実験計画を考えたかどうかを主な評価ポイントにしました。また、どの実験も最終的な不確かさを簡易的に求めることを必須としました。
例えば図は実験に対する誤解をよく表しているおうち実験のレポート例です。いままで「実験の目的はいかに文献値と近い値をだすか」というトレーニングを積んできているため、レポートの結論が「今回の実験は正確だった」になっています。不確かさの評価を行うと同時にこういった実験に対する誤解を解くために、重点的に添削を行いました。
実験の協力者について
実験はそれぞれが別の測定物を用意するという条件で、複数の生徒で協力して実験を行うことを認めました。また、保護者や兄弟に協力してもらうことも歓迎しました。その結果多くの生徒が友達同士で家に集まり実験をしたり、理科に自信のあるお父さんや兄弟に助けてもらって実験を行っていました。中には公園で実験していると、近くを通りかかった人にアドバイスをもらえたというケースもありました。「実験室に閉じない理科、身近な理科」を実践するうえでこのような友達同士や身の回りの人とのコミュニケーションの中に理科実験が組み込まれることは効果が高いと感じています。例えば図3はある生徒のレポートに掲載されていた実験装置図で、工作に自信のあるお父さんに協力してもらい立派な特製坂を制作していました。
実践例
重力加速度測定実験
概要
授業内で扱った等加速度運動を実際に検証してもらう目的として、身の回りの物体を落として落下時間から重力加速度を測定する実験を扱いました。この時
- 落とす高さの不確かさ
- 落下時間の不確かさ
ティッシュを落として実験した例
図3はおうち実験のコンセプトの一つである「実験精度を十分達成できる道具を用意する」という目的に対して典型的な例です。この生徒はマンションの高いところからティッシュを丸めて落として実験を行っています。当然、ティッシュは軽くて測定値が文献値と大きくずれるため、考察でずいぶん苦しんでいるのが印象的でした。既存の実験では落とす物体も教師側が用意するためにこのような壁にぶつかることはありません。ですが、実験物理として初歩的とはいえこのような試行錯誤は重要な経験といえます。(高校生でも空気抵抗を無視できる物体を選ぶべきというのはそこまで自明ではないのです)

凍った缶と凍っていない缶ではどちらがはやく転がるか実験
凍っている物体と凍ってない(液体の)物体のどちらが早く転がるかを調べるために
- 凍った缶
- 凍ってない缶
- 質点の理論値
お父さんと協力して装置を作った例
図4は特に実験装置の組み立てに力を入れた例です。本実験で用意が難しいのが”坂”で、滑り台を利用したり、身の回りの板や細長いものを組み合わせて各々工夫していました。この生徒の場合はおとうさんの協力を得ながら木材を利用して安定した坂を作っており、転がる時間もビデオ測定をしてフレーム数から見積もったりと本格的に頑張っていました。

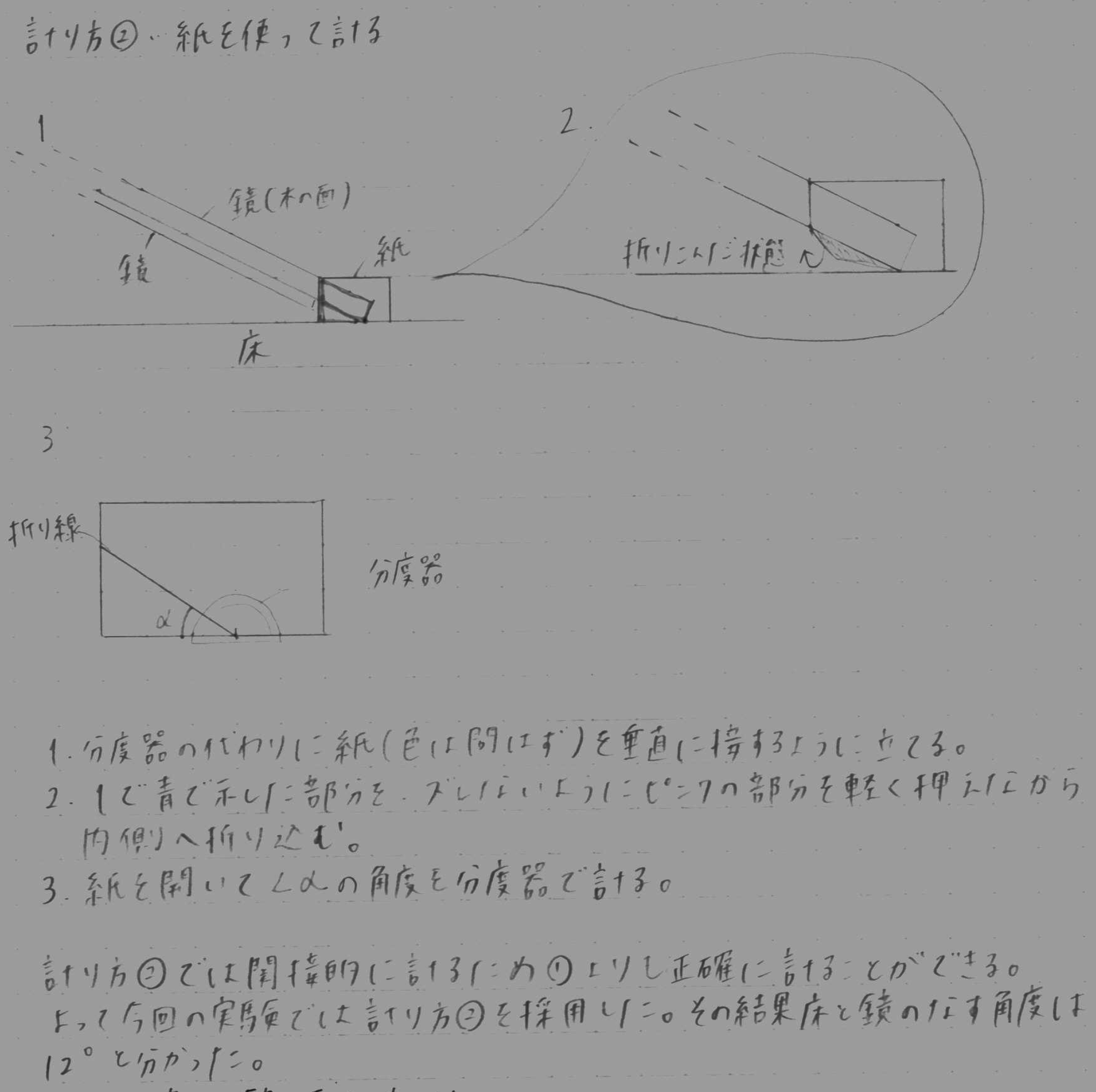
角度の測定を工夫した例
図5は角度の測定を工夫した例です。斜面の角度は分度器を直接当てずらいケースがあります。そこでこの生徒は斜面に対して紙を折り込むことで紙に同じ角度の折り目をつけてそれを測ることで、間接的に角度を測定していました。おうち実験は「実験手順も合理的なように自分で考える」のがポイントの一つです。そのためこのように様々な独自の工夫をみることができました。
角度の測定による系統的な不確かさの見積もりをした例
図6は角度の測定による系統的な不確かさの見積もりをした例です(単位間違いなどが見受けられます)。誤差計算は高校に導入するには難易度が高いので、およそ3度ほどずれうる実験であれば、プラスマイナス3度のケースもそれぞれ計算することでおおまかに見積もるという手法を推奨しています。このように測定値に対して不確かさを必ず見積もるように要請することで、実験が目的に対して十分な精度を持っているのかを考察することができます。